イラストロジックの自動解答アルゴリズム 第1章
- yuji fukami
- 2025年11月12日
- 読了時間: 4分
ペンシルパズルの代表格であるイラストロジックの自動解答プログラムをVBAで構築したので、そのアルゴリズムの紹介。
イラストロジックは別名「NONOGRAM」「ピクロス」などと呼ばれているパズル。正式名称は「NONOGRAM」っぽいですが下記紹介ではイラストロジックと呼んでいきます。
パズルを解いていくと絵柄が浮かび上がってくるもので、自分で解いたときの達成感が魅力のパズルです。
今回はその達成感をぶち壊すことを目的にプログラミングで自動的に解答する方法を解説いたします。
実際にVBAで構築したプログラムをもとにパズルを解答している動画です。
今回解説するアルゴリズムは1ラインだけを解答する場合の処理になります。
処理は「初回解答」と「追加回答」の2つに分かれます。
初回解答
初回解答は最初の空白の状態での解を探索する処理です。
例えば10マスで数字が3,2,1の場合は次のようなアルゴリズムになります。

1マスにおける解答パターンは
「○」→未確定
「・」→白マス
「●」→黒マス
の3種類とします。
数字の3,2,1においてそれぞれ考えられる解答パターンを列挙し、共通するものを解として確定させます。
このときの解答パターンの列挙を「パターン行列」と呼ぶことにします。以後何度も出てきます。
図1の場合は数字3において1つ黒マス「●」が確定します。
追加回答(黒マス)
次の処理が「追加回答」です。
追加回答では例えば横方向で1つでもマスの解が確定した場合、縦方向においてはその確定したマスが追加された解として次の解答で影響を受けてきます。
逆に縦方向で確定した解が、次に横方向で追加された解として次の解答で影響を受けてきます。
追加回答では大きく2種類が考えられます。
・黒マス「●」が追加された場合
・白マス「・」が追加された場合
まず黒マス「●」が追加された場合を考えます。

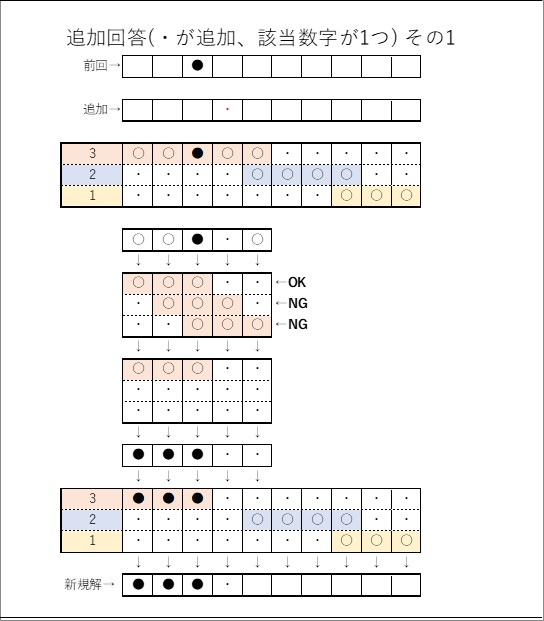
図2の場合だと新しく追加された解に該当するのが数字の3だけになります。
このときは数字の3においてのパターン行列に追加された解を適応すると、3つの解答パターンの内、有効(OK)なものと無効(NG)なものが判別出来ます。
このうち有効なものだけをパターン行列で残し、その有効なパターンにおいて共通するものを新しい確定解として出力します。
つぎに他の位置に黒マスが追加された場合を考えます。

次は数字の1に該当する追加の黒マスです。
この場合は数字の1における解答範囲の終了位置が1つずれるため、数字2,3の解答範囲の終了位置が1つずれて影響されてきます。
このため、各数字の解答範囲の終了位置は常に比較する必要が出てきます。もちろん開始位置も同様です。
つぎに該当する数字が複数ある場合です。

この場合は該当する数字においてそれぞれの数字が該当する場合を仮定して、出力される解の共通部分を新しい解とします。
共通解が無いときもあるので、この処理は面倒くさい割に当たり外れが多いです。
追加回答(白マス)
次に白マス「・」が追加回答にあった場合です。
こちらも黒マス同様に該当する数字でのパターン行列において適応して有効、無効を判断し、有効パターンでの共通事項を新しい解として出力します。
次の場合は数字の解答範囲の開始位置が変化することで、他の数字へ影響する例です。

つぎは該当する数字が複数ある場合です。

この場合は黒マスと異なり、該当する数字においては共通して白マスとして確定するためそれぞれのパターン行列に適応して新しい解を出力させます。
連続黒マスでの可能な数字判定
上記の処理以外に解答を確定させる処理として、連続する黒マスの範囲やその両端の外側1マスにおいて可能な数字の大きさが決まってくる例です。

図8の上側の図では黒マスが2つ続いていますが、この黒マスの範囲に該当する数字は2以上、その両端の外側1マスには3以上が該当するようになります。
黒マスが4つ続く場合は下側の図のようになり、黒鱒の範囲には数字の4以上、その両端の外側には5以上が該当します。
このようにして、黒マスの連続より特定の数字のパターン行列において白マスを確定することが出来たりします。
さらに、黒マスが飛び飛びの場合は次のようになります。
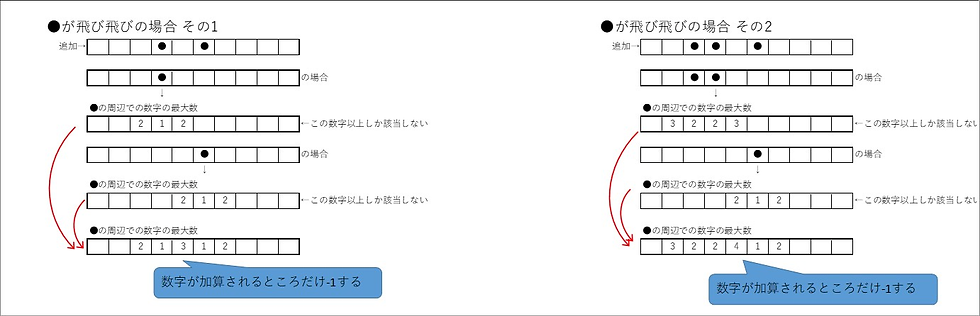
この場合は、それぞれ連続する黒マスの周りの最大可能数字を足し合わせて、加算される部分だけを-1した数がそのマスでの可能な数字の最大になります。
1章まとめ
今回は1ラインでの解答での基本的なアルゴリズムの紹介でした。
次回はこのアルゴリズムをプログラムとして構築するために行列演算を適応する方法の解説です。
第2章へ
イラストロジックの自動解答アルゴリズム 第2章