三次元ベクトル演算用クラスモジュール|Excel VBA(clsVector3D)
- yuji fukami
- 1月27日
- 読了時間: 7分

1. 概要(三次元ベクトル演算用クラスモジュール)
今回は、Excel VBA で 三次元ベクトルの演算を効率的に扱うためのクラスモジュールを紹介します。
別記事の「二次元ベクトル演算用クラスモジュール」と同様に今度は三次元ベクトルの演算を効率的に行えるクラスモジュールとなります。
二次元ベクトル演算用クラスモジュール|Excel VBA
三次元ベクトルの加算・減算・スカラー倍・内積・外積・単位ベクトル化・回転・角度取得といった処理は、通常は数式をその都度コード上に記述する必要があります。
本クラスモジュールでは、これらの演算を オブジェクト指向的にひとつのクラスへまとめて管理することで、
数式を直接書かなくても直感的に処理できる
三次元ベクトル演算の意図がコードから読み取りやすくなる
同じ計算ロジックを何度も使い回せる
といったメリットがあります。
三次元ベクトルを 1つのオブジェクトとして扱えるようになるため、座標計算・方向判定・角度計算・回転処理・法線ベクトルの算出などを含むロジックを、シンプルかつ安全に実装できるようになります。
2.インポート用ファイルダウンロード
本記事で紹介している二次元ベクトル演算クラスは、クラスモジュール(clsVector2D)として配布しています。
まずは、下記の ZIP ファイルをダウンロードしてください。
ZIP ファイルを解凍すると、clsVector3D.cls という クラスモジュール用ファイルが含まれています。
クラスモジュールのインポート手順
ダウンロードした ZIP ファイルを解凍する
Excel を起動し、対象のブックを開く
Alt + F11 を押して VBA エディタを起動する
プロジェクトエクスプローラーを表示する(表示されていない場合は Ctrl + R)
解凍した clsVector3D.cls ファイルを、プロジェクトエクスプローラー内へドラッグ&ドロップする
正常にインポートされると、プロジェクトエクスプローラーの 「クラス モジュール」配下にclsVector3D が追加されます。

3.実際の使い方
本章では、三次元ベクトルの基本的な数式と対応させながら、このクラス内で定義している各プロパティ・メソッドが「どのような演算を担当しているのか」を整理して解説します。
まず「clsVector3D」が使えるようになった前提で下記のサンプルコードを実行してください。
慣れている人でしたらコメントを追えば、どのタイミングでどのメソッド・プロパティを使っているかは、コードを読み慣れている方であれば概ね把握できると思います。

3-1. ベクトルの基本構造(X, Y, Z)
本クラスでは、三次元ベクトル

を、
PriX:X成分
PriY:Y成分
PriZ:Z成分
として内部に保持しています。
また、SetXYZ メソッドは 座標を保持するだけでなく、ノルム(大きさ)も同時に計算して保持する 役割を持ちます。
Call VectorA.SetXYZ(3, 0, 4) ' A = (3, 0, 4)
Call VectorB.SetXYZ(2, 3, 1) ' B = (2, 3, 1)この時点で、X/Y/Z はそれぞれ X, Y, Z プロパティから取得できます。
Debug.Print "VectorA:"; "X = " & VectorA.X, "Y = " & VectorA.Y, "Z = " & VectorA.Z
Debug.Print "VectorB:"; "X = " & VectorB.X, "Y = " & VectorB.Y, "Z = " & VectorB.Z3-2. ノルム(Norm)
ノルムは、三次元ベクトルの長さ(大きさ)を表します。

クラス内では、この値を PriNorm として保持し、Norm プロパティから取得できるようにしています。
Debug.Print "|A| = " & VectorA.Norm
Debug.Print "|B| = " & VectorB.Norm今回の A=(3,0,4) の場合は、

となるため、VectorA.Norm は 5 になります。(毎回計算せず、SetXYZ 時に計算して保持することで、参照処理を軽くしています)
3-3. 単位ベクトル(Unit)
単位ベクトルは、方向はそのままで長さを 1 に正規化したベクトルです。

クラスでは Unit プロパティとして実装しており、結果は 新しい clsVector3D として返します。
Dim UnitA As clsVector3D
Dim UnitB As clsVector3D
Set UnitA = VectorA.Unit
Set UnitB = VectorB.Unit
Debug.Print "UnitA:" & "X = " & UnitA.X, "Y = " & UnitA.Y, "Z = " & UnitA.Z
Debug.Print "UnitB:" & "X = " & UnitB.X, "Y = " & UnitB.Y, "Z = " & UnitB.Zまた PriNorm = 0(0ベクトル)の場合は、0除算を避けるため (0,0,0) を返す実装になっています。
3-4. 加算(Add)・減算(Dif)・スカラー倍(Mult)
■ 加算:C = A + B

Dim Result As clsVector3D
Set Result = VectorA.Add(VectorB)
Debug.Print "C:"; "X = " & Result.X, "Y = " & Result.Y, "Z = " & Result.Z■ 減算:D = A - B

Set Result = VectorA.Dif(VectorB)
Debug.Print "D:"; "X = " & Result.X, "Y = " & Result.Y, "Z = " & Result.Z
■ スカラー倍:E = A × k

Dim k As Double: k = 2
Set Result = VectorA.Mult(k)
Debug.Print "E:"; "X = " & Result.X, "Y = " & Result.Y, "Z = " & Result.Z
これらは「計算の結果を新しいベクトルとして返す」ため、元のベクトルを破壊せずに連鎖的に計算しやすい形になっています。
3-5. 内積(InnerProduct)
内積は、二つのベクトルの“向きの近さ”を表す演算で、

となります。
Dim Dot As Double
Dot = VectorA.InnerProduct(VectorB)
Debug.Print "A・B=" & Dot内積は、次に説明する「角度計算」や「射影(垂直成分の算出)」でも重要な基礎になります。
3-6. 外積(CrossProduct)
三次元ベクトルならではの代表的な演算が「外積」です。外積は、2つのベクトルに垂直なベクトル(法線)を返します。

Dim Cross As clsVector3D
Set Cross = VectorA.CrossProduct(VectorB)
Debug.Print "A×B:"; "X = " & Cross.X, "Y = " & Cross.Y, "Z = " & Cross.Z例えば、3Dで「面の向き」「法線ベクトル」「回転方向(右ねじ)」を扱う場合、外積が頻繁に登場します。2Dのときよりも「別の演算が必要になる」代表例がこの外積です。
3-7. 任意ベクトルとなす角(CalAngleWithVector)
2つのベクトルがなす角 θ\thetaθ は、単位ベクトル同士の内積を使うと求められます。

クラスでは CalAngleWithVector として実装しており、ラジアンで返します。
Dim AngleRad As Double
AngleRad = VectorA.CalAngleWithVector(VectorB)
Debug.Print "Angle(A,B) = " & AngleRad & " (rad)"
Debug.Print "Angle(A,B) = " & (AngleRad * 180 / WorksheetFunction.Pi) & " (deg)"「度数法(deg)」で見たい場合は、上記のように * 180 / Pi で変換します。
3-8. 回転(RotateX / RotateY / RotateZ / RotateXYZ)
三次元ベクトルでは、回転は「どの軸の周りに回すか」で式が変わります。
■ X軸回り回転(RotateX)
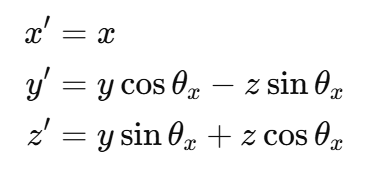
Dim ThetaX As Double
ThetaX = WorksheetFunction.Pi / 2
Set Result = VectorA.RotateX(ThetaX)
Debug.Print "A':"; "X = " & Result.X, "Y = " & Result.Y, "Z = " & Result.Z■ Y軸回り回転(RotateY)

Dim ThetaY As Double
ThetaY = WorksheetFunction.Pi / 6
Set Result = VectorA.RotateY(ThetaY)
Debug.Print "A':"; "X = " & Result.X, "Y = " & Result.Y, "Z = " & Result.Z■ Z軸回り回転(RotateZ)

Dim ThetaZ As Double
ThetaZ = WorksheetFunction.Pi / 3
Set Result = VectorA.RotateZ(ThetaZ)
Debug.Print "A':"; "X = " & Result.X, "Y = " & Result.Y, "Z = " & Result.Z■ XYZ回転(RotateXYZ)
RotateXYZ は内部で
Z軸回転 → Y軸回転 → X軸回転
の順で適用しています(合成回転は順序依存です)。
Set Result = VectorA.RotateXYZ(ThetaX, ThetaY, ThetaZ)
Debug.Print "A':"; "X = " & Result.X, "Y = " & Result.Y, "Z = " & Result.Z3-9. 配列出力(Array1D / Array2D)
ベクトルは最終的に「配列」や「シート出力」へ変換したくなる場面が多いです。本クラスでは、用途別に2種類の形式で取り出せます。
■ Array1D(一次元配列)

Dim Arr1 As Variant
Arr1 = VectorA.Array1D
Debug.Print "{" & Arr1(1) & ", " & Arr1(2) & ", " & Arr1(3) & "}"■ Array2D(二次元配列)

Dim Arr2 As Variant
Arr2 = VectorA.Array2D
Debug.Print "(" & Arr2(1, 1) & ")"
Debug.Print "(" & Arr2(2, 1) & ")"
Debug.Print "(" & Arr2(3, 1) & ")"特に Array2D は縦方向にRangeへ一括貼り付けしやすい形です。
3-10. 任意方向に対する垂直成分方向(CalVerticalVector)
CalVerticalVector は「自分自身(Vec1)に対して、Vec2 の垂直成分方向(単位ベクトル)」を返すメソッドです。
直感的には、
Vec2 を Vec1 に射影した成分を引き算し
Vec1 に直交する方向成分だけを取り出す
という処理になります。

Dim VerticalDir As clsVector3D
Set VerticalDir = VectorA.CalVerticalVector(VectorB)
Debug.Print "出力:"; "X = " & VerticalDir.X, "Y = " & VerticalDir.Y, "Z = " & VerticalDir.Z
ただし実装上、Vec1 と Vec2 が平行(内積が ±1)だと垂直方向が定義できないため、メッセージ表示して終了します。
3-11. Show(座標の表示)
最後に Show は、座標をイミディエイトウィンドウへ出力します。デバッグ時に「いまのXYZをサッと確認したい」用途で便利です。
Debug.Print "VectorA.Show"
VectorA.Show
Debug.Print "VectorB.Show"
VectorB.Show4. clsVector3Dを使わない場合との比較
ここでは、同じ処理を「clsVector3Dを使う場合」と、「使わない場合(配列で計算する場合)」で比較します。やることはどちらも同じです。
ベクトルA = (3, 0, 4)、ベクトルB = (2, 3, 1) を用意
それぞれ 2 倍する(スカラー倍)
2倍したベクトル同士の 外積 を求める(=垂直方向ベクトル)
外積結果が本当に垂直か、内積で確認(=0 になる)
4-1. clsVector3Dを使う場合(読みやすく、1行でつながる)
「2倍したAと2倍したBの外積」 という意図が、A.Mult(2).CrossProduct(B.Mult(2)) の 1行でそのまま表現できています。
4-2. clsVector3Dを使わない場合(配列+成分計算が散らばる)
4-3. 比較まとめ(どこが面倒になるか)
クラスを使わない場合は、どうしても次のような記述が増えます。
ベクトルを 配列で保持する必要がある
スカラー倍のたびに X/Y/Z を別々に計算して代入する必要がある
外積は式が長く、成分ごとの計算が散らばる
単位ベクトル化も、ノルム計算→除算→0判定が必要になる
演算が増えるほど、変数・配列・代入が増えてコードが散らかる
一方で clsVector3D を使うと、
「スカラー倍」「外積」「単位ベクトル化」などの演算を メソッドとして意味ごとまとめられる
A.Mult(2).CrossProduct(B.Mult(2)).Unit のように 直感的に連結できる
数式(成分計算)を書かずに、処理の意図がコード上に残る
というメリットが出ます。

